MathPrompter: 数学推理

该文介绍了 MathPrompter: 数学推理 框架，解决需要多步推理的复杂数学问题。

论文要解决的问题

（1）数学问题通常只有一个正确答案，对于一个需要多步推理的复杂数学问题，语言模型通常都无法给出正确答案，即便有「思维链」技术的加持，往往中间步骤也会出错。
（2）并且，在数学问题上，现有的语言模型通常不会对自己的答案提供置信度（confidence），让用户无从判断生成答案的可信度。

采用方法

（1）MathPrompter 使用 Zero-shot 思维链提示技术生成多个代数表达式或 Python 函数，以不同方式解决同一个数学问题，从而提高输出结果的可信度。
（2）相比其他基于提示的 CoT 方法，MathPrompter 还会检查中间步骤的有效性。

结果

基于 175B 参数 GPT，使用 MathPrompter 方法将MultiArith 数据集的准确率从 78.7% 提升到了 92.5%。

---

1 专攻数学的Prompt

最近自然语言处理的发展很大程度上归功于大型语言模型（LLMs）在规模上的不断扩展，其展现出了惊人的 zero-shot 和 few-shot 能力，也促成了 prompting 技术的发展，用户只需要在 prompt中给 LLM 输入几个简单的样例即可对新任务进行预测。prompt 对于单步的任务相当成功，但在需要多步骤推理的任务中，提示技术的性能仍然不够。

人类在解决一个复杂问题时，会将其进行分解，并尝试一步步地解决，思维链（CoT）提示技术就是将这种直觉扩展到 LLMs 中，在一系列需要推理的NLP任务中都得到了性能改进。

本篇论文主要研究用于解决数学推理任务的 Zero-shot-CoT 方法，之前的工作已经在 MultiArith 数据集上得到了显著的准确率改进，从 $17.7\%$ 提升到了 $78.7\%$，但仍然存在两个关键的不足之处：
（1）虽然模型所遵循的思维链改进了结果，但却没有检查思维链提示所遵循的每个步骤的有效性；
（2）没有对LLM预测结果提供置信度（confidence）。

2 MathPrompter

为了在一定程度上解决上述差距，从人类解决数学题的方式中得到启发，将复杂问题分解为更简单的多步程序，并利用多种方式在每一个步骤中对方法进行验证。

图2.1 MathPrompter 工作流

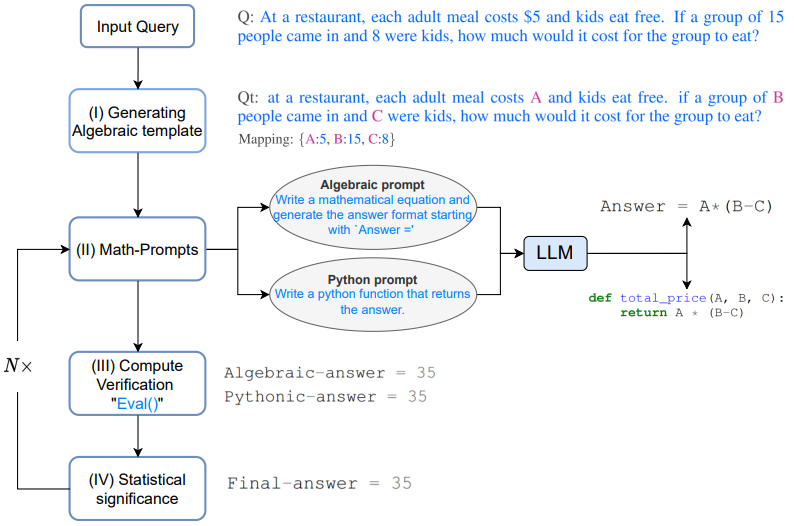
由于LLM是生成式模型，要确保生成的答案是准确的，特别是对于数学推理任务，就变得非常棘手。通过观察学生解决算术问题的过程，总结出了学生为验证其解决方案而采取的几个步骤：
（1）遵循已知结果（Compliance with known results），通过将解决方案与已知结果进行比较，可以评估其准确性并进行必要的调整；当问题是一个具有成熟解决方案的标准问题时，这一点尤其有用。
（2）多重验证 （Multi-verification），通过从多个角度切入问题并比较结果，有助于确认解决方案的有效性，确保其既合理又准确。
（3）交叉检查 （Cross-checking），解决问题的过程与最终的答案同样必要；验证过程中的中间步骤的正确性可以清楚地了解解决方案背后的思维过程。
（4）计算验证 （Compute verification），利用计算器或电脑进行算术计算可以帮助验证最终答案的准确性。

具体而言，给定一个问题 $Q$。

Q:At a restaurant, each adult meal costs \$5 and kids eat free. If a group of 15people came in and 8 were kids, how much would it cost for the group to eat？

在一家餐厅，每份成人餐的价格是5美元，儿童免费用餐。如果有15个人进来，其中8个是孩子，那么这群人要花多少钱吃饭？

2.1 生成代数模板 Generating Algebraic template

首先将问题转化为代数形式，通过使用键值映射将数字项替换为变量，然后得到修改后的问题 $Qt$。

Qt: at a restaurant, each adult meal costs A and kids eat free. if a group of B people came in and C were kids, how much would it cost for the group to eat？

Mapping：{A：5， B：15， C：8}

2.2 数学提示 Math-prompts

基于上述多重验证和交叉检查的思维过程所提供的直觉上，使用两种不同的方法生成 Qt 的分析解决方案，即代数方式和 Pythonic 方式，给 LLM 提供以下提示，为 Qt 生成额外的上下文。

Algebraic prompt: Write a mathematical equation and generate the answer format starting with 'Answer ='

Python prompt: Write a Python function that returns the answer.

提示可以是推导出一个代数表达式或编写一个Python函数
LLM 模型在响应提示后可以输出如下表达式。

# Algebraic expression output
Answer = A * (B - C)

# Python expression output
def total_price(A, B, C): 
    return A * (B - C)

上述生成的分析方案为用户提供了关于LLM的「中间思维过程」的提示，加入额外的提示可以提高结果的准确性和一致性，反过来会提高MathPrompter生成更精确和有效的解决方案的能力。

2.3 计算验证 Compute verification

使用 Qt 中输入变量的多个随机键值映射来评估上一步生成的表达式，使用 Python 的 eval() 方法对这些表达式进行评估。
然后比较输出结果，看是否能在答案中找到一个共识（consensus），也可以提供更高的置信度，即答案是正确且可靠的。

Algebraic-answer = 35
Pythonic-answer = 35

一旦表达式在输出上达成一致，就使用输入 $Q$ 中的变量值来计算最终的答案。

2.4 统计学意义 Statistical significance

为了保证各种表达式的输出结果达成共识，实验中将步骤2和3重复大约5次，并记录出现最频繁的答案值。在没有明确共识的情况下，重复步骤2、3、4。

3 实验结果

在 MultiArith 数据集上对 MathPrompter 进行评估，其中的数学问题专门用来测试机器学习模型进行复杂算术运算和推理的能力，要求应用多种算术运算和逻辑推理才能成功地解决。

图3.1 MultiArith实验结果

在 MultiArith 数据集上的准确率结果显示，MathPrompter的表现优于所有的 Zero-shot 和 Zero-shot-CoT 基线，将准确率从 $78.7\%$ 提升到 $92.5\%$

可以看到，基于 $175B$ 参数 GPT3 DaVinci 的 MathPrompter 模型的性能与 $540B$ 参数模型以及 SOTA 的 Few-shot-CoT 方法相当。

图3.2 效果比较

从上表可以看到，MathPrompter的设计可以弥补生成的答案有时会有一步之差的问题，可以通过多次运行模型并报告共识结果来避免。

此外，推理步骤可能过于冗长的问题，可以由 Pythonic 或Algebraic 方法可以解决这个问题，通常需要较少的 token。

此外，推理步骤可能是正确的，但最终的计算结果却不正确，MathPrompter 通过使用 Python 的 eval() 方法函数来解决这个问题。

在大部分情况下，MathPrompter 都能生成正确的中间和最终答案，不过也有少数情况，如表中的最后一个问题，代数和 Pythonic 的输出都是一致的，但却有错误。