近似最近邻搜索算法Annoy
近似最近邻搜索算法Annoy
本文以 中的点集来作为案例,介绍 Annoy(APPROXIMATE NEAREST NEIGHBORS OH YEAH)算法的基本思想和算法原理。
用 n 表示现有的文档个数,如果采用暴力搜索的方式,那么每次查询的耗时是 O(n), 采用合适的数据结构可以有效地减少查询的耗时,在 annoy 算法中,作者采用了二叉树这个数据结构来提升查询的效率,目标是把查询的耗时减少至 O(ln(n)).
1 构建二叉树索引
刚开始的时候,在数据集中随机选择两个点,然后用它们的中垂线来切分整个数据集,于是数据集就被分成了蓝绿两个部分。然后再随机两个平面中各选出一个顶点,再用中垂线进行切分,于是,整个平面就被切成了四份。
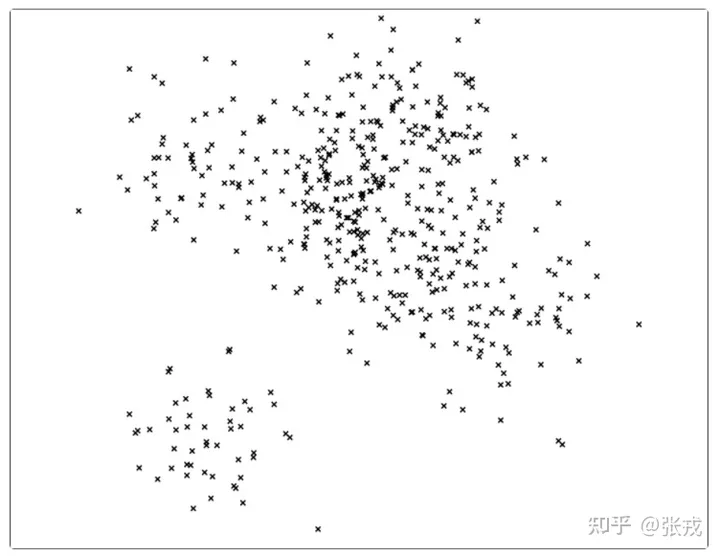

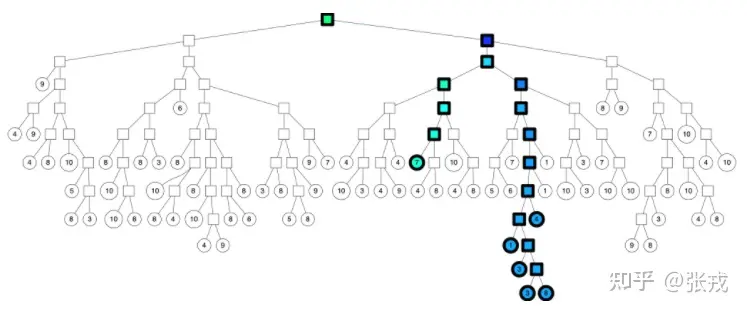
用一颗二叉树来表示这个被切分的平面就是:
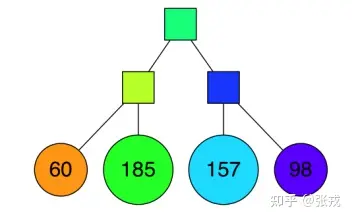
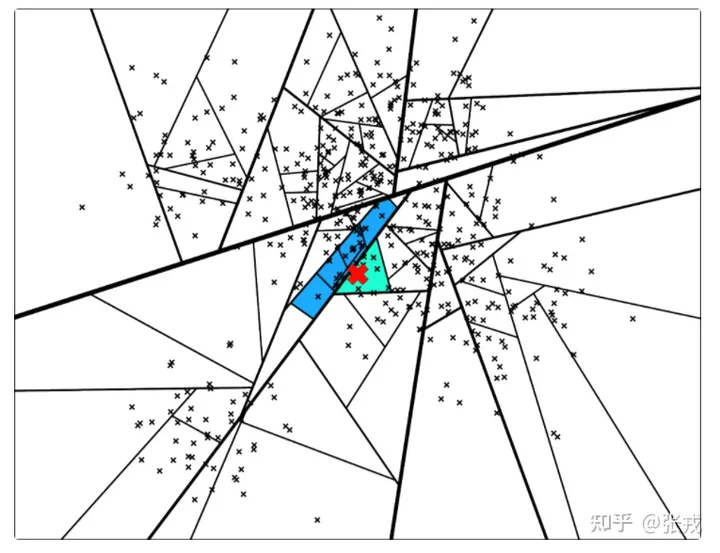
后续继续采用同样的方式进行切分,直到每一个平面区域最多拥有 K 个点为止。当 K = 10 时,其相应的切分平面和二叉树如下图所示。

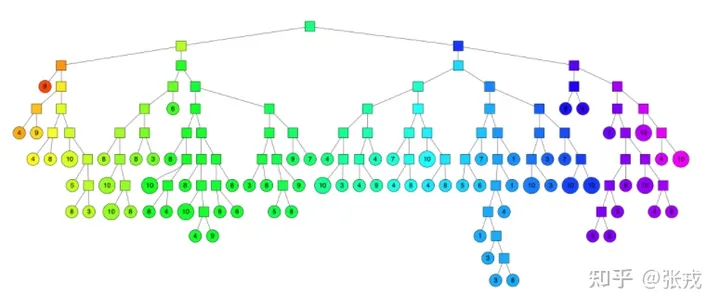
下面,新来的一个点(用红色的叉表示),通过对二叉树的查找,我们可以找到所在的子平面,然后里面最多有 K = 10 个点。从二叉树的叶子节点来看,该区域只有 7 个点。
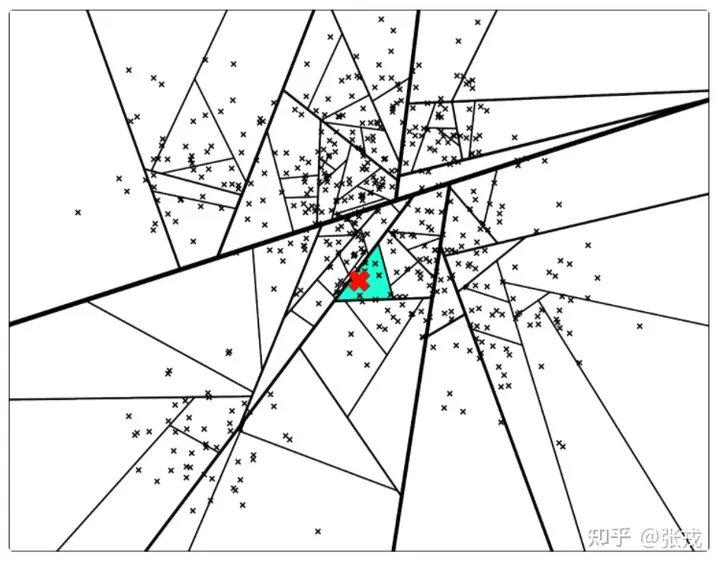
在 ANN 领域,最常见的两个问题是:
(1)如果我们想要 Top K 的点,但是该区域的点集数量不足 K,该怎么办?
(2)如果真实的 Top K 中部分点不在这个区域,该怎么办?
作者用了两个技巧来解决这个问题:
1.使用优先队列(priority queue):将多棵树放入优先队列,逐一处理;并且通过阈值设定的方式,如果查询的点与二叉树中某个节点比较相似,那么就同时走两个分支,而不是只走一个分支;
2.使用森林(forest of trees):构建多棵树,采用多个树同时搜索的方式,得到候选集 Top M(M > K),然后对这 M 个候选集计算其相似度或者距离,最终进行排序就可以得到近似 Top K 的结果。
同时走两个分支的的示意图:
随机生成多棵树,构建森林的示意图:

2 算法原理:
构建索引:建立多颗二叉树,每颗二叉树都是随机切分的;
查询方法:
(1)将每一颗树的根节点插入优先队列;
(2)搜索优先队列中的每一颗二叉树,每一颗二叉树都可以得到最多 Top K 的候选集;
(3)删除重复的候选集;
(4)计算候选集与查询点的相似度或者距离;
(5)返回 Top K 的集合。
