向量检索：从Delaunay graph到HNSW Graph

ANN最近邻搜索广泛应用在各类搜索、分类任务中，在超大的数据集上因为效率原因转化为ANN，常见的算法有KD树、LSH、IVFPQ和本文提到的HNSW。

向量检索分为暴力求解的KNN和近似求解的ANN算法，其中ANN又可分为以下几类：
（1）基于树：KDTree、Annoy；
（2）基于哈希：LSH；
（3）基于量化：PQ；
（4）基于图：NSW，HNSW。
HNSW（Hierarchical Navigable Small World）是ANN搜索领域基于图的算法，我们要做的是把D维空间中所有的向量构建成一张相互联通的图，并基于这张图搜索某个顶点的K个最近邻，如下图所示：

图1.1 D维空间中的点进行构图示意图

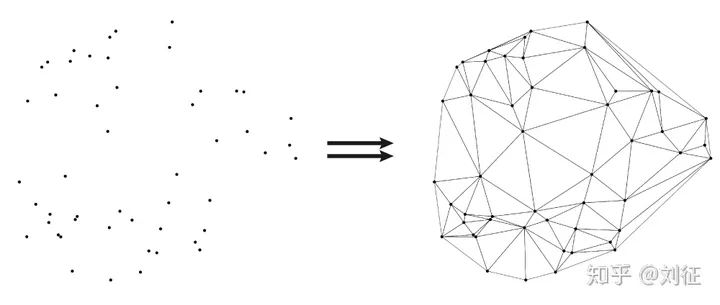
1 Delaunay graph

说起HNSW，就不能不提前作NSW，在NSW中作者建立了一个类Delaunay graph，所以这里先看了下Delaunay graph。
Delaunay graph的构建流程如下：
（1）构造一个超级三角形，包含所有散点，放入三角形链表；
（2）将点集中的散点依次插入，在三角形链表中找出其外接圆包含插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，从而完成一个点在 Delaunay 三角形链表中的插入；
（3）根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入 Delaunay 三角形链表；
（4）循环执行上述第 2 步，直到所有散点插入完毕。

图1.2 Delaunay graph构建第2步示意图

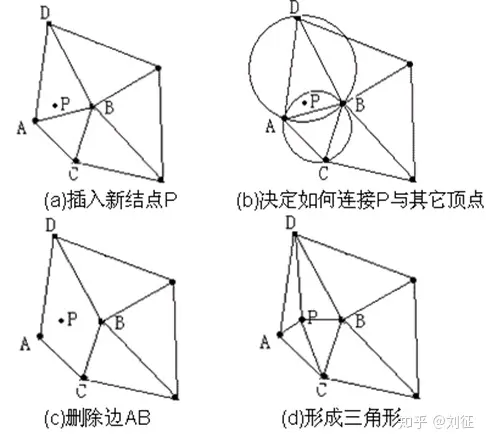
形成的Delaunay graph有这些优点：图中每个点都有“友点”，不会有“孤点”存在，导致无法搜索到；相近的点都互为“友点”，保证了搜索结果的准确性；图中所有连接（线段）的数量最少，保证了搜索的效率。

2 NSW Graph

NSW没有采用这种方式进行建图，原因是这种建图方式建图和搜索的时间复杂度太高，NSW的建图方式非常简单，就是向图中插入新点时，通过随机存在的一个点出发查找到距离新点最近的m个点（m由用户设置），连接新点到这最近的m个点。

图2.1 NSW Graph插入节点示意图

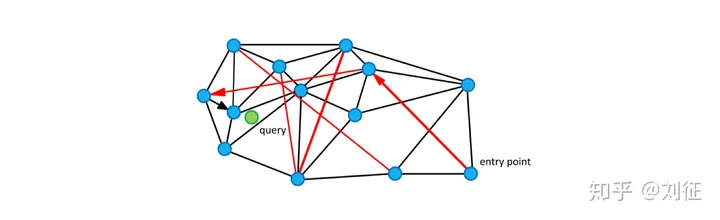
NSW论文中配了这样一张图，黑色是近邻点的连线，红色线就是“高速公路机制”了。我们从enter point点进入查找，查找绿色点临近节点的时候，就可以用过红色连线“高速公路机制”快速查找到结果。高速公路是怎么形成的呢？在初始建图时，点还很少，这时连接的m个点在建图后期中间可能加入了成千上万个点，所以在建图初期连接的这些边就自然变成了“高速公路”。
对于查询来说，这里有三个点集合：candidates、visitedset、results 。其中candidates为当前要考察的点集合，visitedset为已经访问过的点集合，results为当前距离查询点最近的点集合；前两者为变长，最后为定长。
查询流程如下：
（1）随机选择一个点作为查询起始点entry_point，把该点加入candidates中，同时加入visitedset；
（2）遍历candidates，从candidates中选择距离查询点最近的点c，和results中距离查询点最远的点d进行比较，如果c和查询点q的距离大于d和查询点q的距离，则结束查询，说明当前图中所有距离查询点最近的点已经都找到了，或者candidates为空；
（3）从candidates中删除点c；
（4）查询c的所有邻居e，如果e已经在visitedset中存在则跳过，不存在则加入visitedset；
（5）把比d和q距离更近的e加入candidates、results中，如果results未满，则把所有的e都加入candidates、results。如果results已满，则弹出和q距离最远的点；
（6）循环（2）-（5）。
论文中的伪码：

K-NNSearch(object q, integer: m, k)
TreeSet [object] tempRes, candidates, visitedSet, result 
// 进行m次循环，避免随机性
for (i←0; i < m; i++) do:
    put random entry point in candidates
    tempRes←null
    repeat:
        // 利用上述提到的贪婪搜索算法找到距离q最近的点c
        get element c closest from candidates to q
        remove c from candidates
        // 判断结束条件
        if c is further than k-th element from result then
            break repeat
        // 更新后选择列表
        for every element e from friends of c do:
            if e is not in visitedSet then
                add e to visitedSet, candidates, tempRes
    end repeat
    // 汇总结果
    add objects from tempRes to result 
end for 
return best k elements from result

3 HNSW Graph

HNSW是对NSW的进一步优化，论文中的一张图足以解释HNSW做了什么改变：

图3.1 HNSW示意图

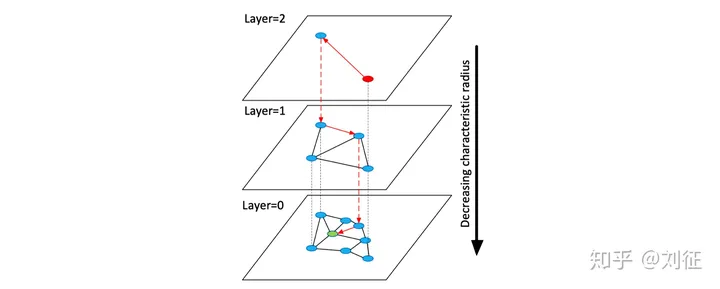
（1）第0层中包含图中所有节点；
（2）向上节点数依次减少，遵循指数衰减概率分布；
（3）建图时新加入的节点由指数衰减概率函数得出该点最高投影到第几层；
（4）从最高的投影层向下的层中该点均存在；
（5）搜索时从上向下依次查询。
这里重点说一下增加节点：

 INSERT(hnsw, q, M, Mmax, efConstruction, mL)
/**
 * 输入
 * hnsw：q插入的目标图
 * q：插入的新元素
 * M：每个点需要与图中其他的点建立的连接数
 * Mmax：最大的连接数，超过则需要进行缩减
 * efConstruction：动态候选元素集合大小
 * mL：选择q的层数时用到的标准化因子
 */
1.先计算这个点可以深入到第几层，lßfloor(-ln(uniform(0,1)) * ml)
2.自顶层向q的层数l逼近搜索，一直到l+1,每层寻找当前层q最近邻的1个点
3.自l层向底层逼近搜索,每层寻找当前层q最近邻的efConstruction个点赋值到集合W
4.在W中选择q最近邻的M个点作为neighbors双向连接起来
5.检查每个neighbors的连接数，如果大于Mmax，则需要缩减连接到最近邻的Mmax个

在某一层中查询最近邻和NSW中的查询算法一致，这里就不重复了
需要注意的是第5点，每个节点的出度是有上限的，这样可以保证搜索的效率，这里就需要针对某些边进行裁剪，那么该裁剪哪些边呢？Fast Approximate Nearest Neighbour Graphs一文中给出了裁边的原则：
edge(p1, p2) occludes edge(p1, p3) if
d(p1, p2) < d(p1, p3) and d(p2, p3) < d(p1, p3)

图3.2 裁剪边示意图

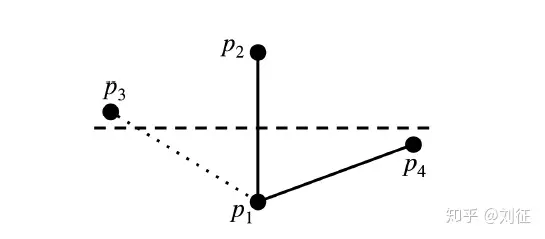
用在这张图上，p1连接了p2、p3、p4，其中p1p3会被裁掉。