GPT2论文分享与架构分析

最后的开神-wkyc大约 6 分钟

GPT2论文分享与架构分析

GPT-2 模型由多层单向 Transformer 的解码器部分构成，本质上是自回归模型，自回归的意思是指，每次产生新单词后，将新单词加到原输入句后面，作为新的输入句。

论文名称：Language Models are Unsupervised Multitask Learners

1 语言建模

作者方法的核心是语言建模。语言建模通常被构造为来自一组示例 $(x_1,x_2,\dots,x_n)$ 的无监督分布估计，每个示例由可变长度的符号序列 $(s_1,s_2,\dots,s_n)$ 组成。由于语言具有自然的顺序性，因此通常将符号上的联合概率分解为条件概率的乘积。

p(x)=\prod\limits_{i=1}^{n}p(s_n|s_1,\dots,s_{n-1}) \tag {1.1}

该方法允许从 $p(x)$ 以及 $p(s_{n-k},\dots,s_n|s_1,\dots,s_{n-k-1})$ 形式的任何条件进行可追踪采样和估计。近年来，可以计算这些条件概率的模型的表达能力有了显著的提高，例如Transformer的Self-Attention架构。

学习执行单个任务可以在概率框架中表示为估计一个条件概率 $p(output|input)$ 。由于一般的系统应该能够执行许多不同的任务，即使对于相同的输入，它不仅应该对输入进行调节，还应该对要执行的任务进行调节。也就是说，它应该建模为 $p(output|input,task)$ 。这在多任务和元学习环境中已被各种形式化。

2 模型架构

该模型在很大程度上遵循OpenAI GPT模型的细节，同时有一些小的改动。LN层被移动到每个子block的输入端，类似于预激活残差网络，并且在最终的Self-Attention块之后添加了额外的LN层。使用修正的初始化，该初始化考虑了模型深度在残差路径上的累积。作者将初始化时残差层的权重按 $\frac{1}{\sqrt{N}}$ 的因子进行缩放，其中N是残差层的数量。词汇表大小扩展到50257。作者还将上下文大小从512个token增加到1024个token，并使用更大的batch size 512。

运行以下程序即可输出模型结构：

from transformers import GPT2LMHeadModel

model = GPT2LMHeadModel.from_pretrained('gpt2')
print(model.modules)

程序输出：

<bound method Module.modules of GPT2LMHeadModel(
  (Transformer): GPT2Model(
    (wte): Embedding(50257, 768)
    (wpe): Embedding(1024, 768)
    (drop): Dropout(p=0.1, inplace=False)
    (h): ModuleList(
      (0-11): GPT2Block(
        (ln_1): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
        (attn): GPT2Attention(
          (c_attn): Conv1D()
          (c_proj): Conv1D()
          (attn_dropout): Dropout(p=0.1, inplace=False)
          (resid_dropout): Dropout(p=0.1, inplace=False)
        )
        (ln_2): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
        (mlp): GPT2MLP(
          (c_fc): Conv1D()
          (c_proj): Conv1D()
          (act): NewGELUActivation()
          (dropout): Dropout(p=0.1, inplace=False)
        )
      )
    )
    (ln_f): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
  )
  (lm_head): Linear(in_features=768, out_features=50257, bias=False)
)>

3 模型架构解析

结合GPT论文给出的模型架构，GPT2论文给出的模型架构改动，和GPT2模型的源码，总结出了如图3.1的GPT2模型结构图。

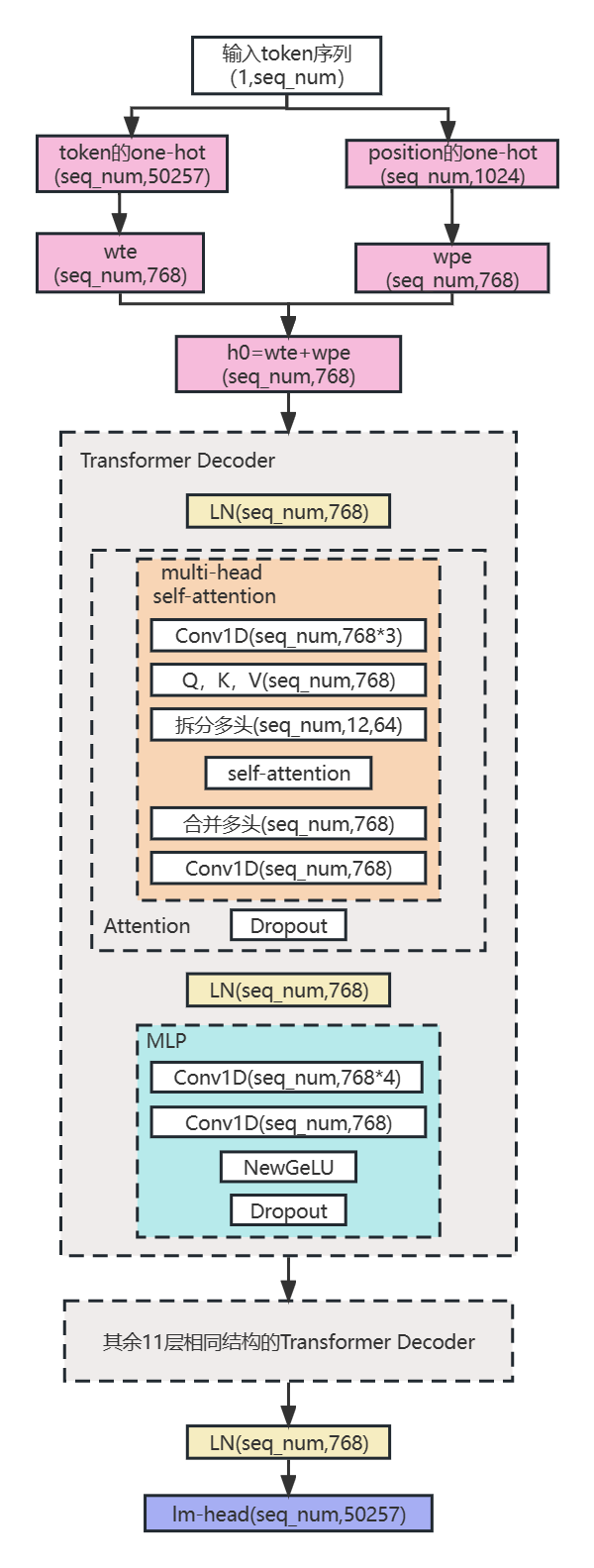
3.1 LN

对向量用以下函数进行了标准化。

y=\frac{x-E(x)}{\sqrt{Var(x)+\epsilon}}{\gamma}+\beta \tag {3.1}

其中是防止分母为0的超参数，，是可训练参数。

一言以蔽之。BN是对batch的维度去做归一化，也就是针对不同样本的同一特征做操作。LN是对hidden的维度去做归一化，也就是针对单个样本的不同特征做操作。因此LN可以不受样本数的限制。

下面举个例子，程序输入：

import torch
from torch import nn

bn = nn.BatchNorm1d(5)  # 实例化一个BN层
ln = nn.LayerNorm(5)  # 实例化一个LN层
x = torch.Tensor([[1,2,3,4,5],
                  [6,7,8,9,10]])

y = ln(x)
z = bn(x)
print(y)
print(z)

程序输出：

tensor([[-1.4142, -0.7071,  0.0000,  0.7071,  1.4142],
        [-1.4142, -0.7071,  0.0000,  0.7071,  1.4142]],
       grad_fn=<NativeLayerNormBackward0>)
tensor([[-1.0000, -1.0000, -1.0000, -1.0000, -1.0000],
        [ 1.0000,  1.0000,  1.0000,  1.0000,  1.0000]],
       grad_fn=<NativeBatchNormBackward0>)

3.2 Multi-head Self-Attention

首先Self-Attention的计算式如式3.2所示。

Attention(Q,K,V)=\rm{softmax}(\frac{QK^T}{\sqrt{d_k}})V \tag{3.2}

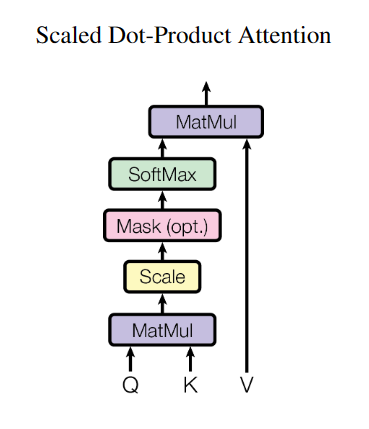
其中Q，K，V是三个矩阵分别与输入x做矩阵乘法的结果，本质上都是x的线性变换。是K的维度。

而Multi-head Self-Attention结构如下图所示。

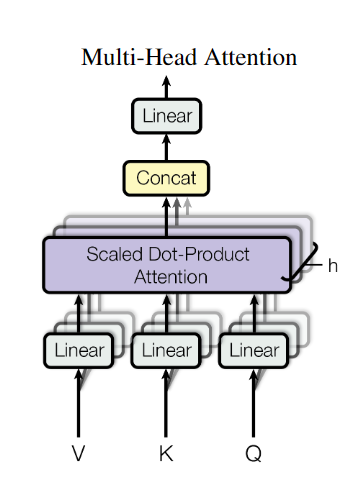
他把Q，K，V在最后一个维度平等的拆分，然后平行地经过Self-Attention计算，再然后合并，最后经过一层线性层输出。

3.3 GPT2Attention

首先结构如下所示。

(attn): GPT2Attention(
  (c_attn): Conv1D()
  (c_proj): Conv1D()
  (attn_dropout): Dropout(p=0.1, inplace=False)
  (resid_dropout): Dropout(p=0.1, inplace=False)
)

模型中的Conv1D层并非pytorch预设的卷积层torch.nn.Conv1d，而是OpenAI自定义的一个卷积层。

定义如下所示。

class Conv1D(nn.Module):
    def __init__(self, nf, nx):
        super().__init__()
        self.nf = nf
        w = torch.empty(nx, nf)
        nn.init.normal_(w, std=0.02)
        self.weight = nn.Parameter(w)
        self.bias = nn.Parameter(torch.zeros(nf))

    def forward(self, x):
        size_out = x.size()[:-1] + (self.nf,)
        x = torch.addmm(self.bias, x.view(-1, x.size(-1)), self.weight)
        x = x.view(size_out)
        return x

其中nf，nx是构造参数，weight和bias有可训练参数，总共nf*nx+nf个。

对他进行了一下测试，测试程序如下所示。

cv = Conv1D(18, 6)  # 实例化一个Conv1D对象

x = torch.Tensor([[1, 2, 3, 4, 5, 6]])
y = cv(x)
print('y:', y)

程序输出如下所示。

y: tensor([[ 0.0829,  0.2766, -0.0990, -0.1236, -0.0434, -0.0720, -0.0817,  0.1380, -0.2762,  0.1568,  0.1062, -0.0501, -0.2094,  0.1371, -0.3037, -0.0866, 0.2650,  0.1390]], grad_fn=<ViewBackward0>)

输入1行6列的矩阵，输出了1行18列的矩阵。

从代码来看，通过Attention层的第一个Conv1D，768列的矩阵会被扩增为为列的矩阵，然后马上会切分到三个768列的矩阵然后分别作为Q，K，V加入Self-Attention计算。因此，Attention层的第一个Conv1D相当于是集成了从输入x到Q，K，V的三个线性变换。

在Attention层的两个Conv1D之间，进行了multi-headed Self-Attention的计算和拼接，此时拼接完之后已经变回了768列的矩阵。

通过Attention层的第二个Conv1D，其源码参数nf，nx均为768，768列的矩阵向768列的矩阵进行了一个线性变换。该层执行了multi-head Self-Attention的最后的Linear层的工作。

3.4 参数量计算

wte：50257*768=38,597,376
wpe：1024*768=786,432
每个Dropout：0
每个LN：768*2=1,536
每个NewGELUActivation：0
每个GPT2Attention中的第一个Conv1D：768*3*768+768*3=1,771,776
每个GPT2Attention中的第二个Conv1D：768*768+768=590,592
每个GPT2MLP中的第一个Conv1D：768*4*768+768*4=2,362,368
每个GPT2MLP中的第二个Conv1D：768*768*4+768=2,360,064
每个GPT2Attention：1,771,776+590,592=2,362,368
每个GPT2MLP：2,362,368+2,360,064=4,722,432
每个GPT2Block：2,362,368+4,722,432+1536*2=7,087,872
lm_head：768*50257=38,597,376
总参数量：wte+wpe+GPT2Block*12+LN+lm_head=124,439,808

GPT2论文分享与架构分析

# GPT2论文分享与架构分析

# 1 语言建模

# 2 模型架构

# 3 模型架构解析

# 3.1 LN

# 3.2 Multi-head Self-Attention

# 3.3 GPT2Attention

# 3.4 参数量计算

GPT2论文分享与架构分析

1 语言建模

2 模型架构

3 模型架构解析

3.1 LN

3.2 Multi-head Self-Attention

3.3 GPT2Attention

3.4 参数量计算