机器学习之强化学习中的策略学习

猞猁-zlj大约 4 分钟

基于价值的（Policy-Based）方法直接输出下一步动作的概率，根据概率来选取动作。但不一定概率最高就会选择该动作，还是会从整体进行考虑。适用于非连续和连续的动作。常见的方法有Policy gradients。

1 策略梯度算法

1.1 算法核心思想

参数为的 $\theta$ 策略接受状态s，输出动作概率分布，在动作概率分布中采样动作，执行动作(形成运动轨迹 $\tau$ )，得到奖励，跳到下一个状态 $s'$ 。
在这样的步骤下，可以使用策略 $\pi$ 收集一批样本，然后使用梯度下降算法学习这些样本，不过当策略 $\pi$ 的参数更新后，这些样本不能继续被使用，还要重新使用策略 $\pi$ 与环境互动收集数据。
在ChatGPT中参数为 $\theta$ 的神经网络对应RL微调的SFT模型，参数为 $\theta'$ 的模型对应专门采样的另一个SFT模型，动作a可以理解为回答问题输出token，s为回答问题之前的状态， $s'$ 为回答问题之后的状态。

1.2 评价标准

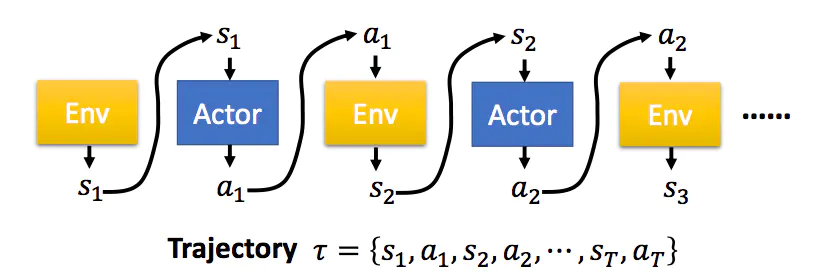
给定智能体或演员的策略参数 $\theta$ ，可以计算某一条轨迹 $\tau$ 发生的概率为轨迹 $\tau$ 来源于在特定的环境状态下采取特定动作的序列，而特定的状态、特定的动作又分别采样自智能体的动作概率分布 $p_{\theta}(a_{t}|s_{t})$ 、状态的转换概率分布 $p(s_{t+1}|s_t,a_t)$ 。

\begin{aligned} p_{\theta}(\tau)& =p(s_1)p_\theta(a_1|s_1)p(s_2|s_1,a_1)p_\theta(a_2|s_2)p(s_2|s_1,a_1)\cdotp\cdotp\cdotp \\ &=p(s_1)\prod_{t=1}^Tp_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t) \end{aligned} \tag {1.1}

由于每一个轨迹 $\tau$ 都有其对应的发生概率，对所有 $\tau$ 出现的概率与对应的奖励进行加权最后求和，即可得期望值。

\overline{R}_\theta=\sum_\tau R(\tau)p_\theta(\tau)=E_{\tau\sim p_\theta(\tau)}[R(\tau)] \tag {1.2}

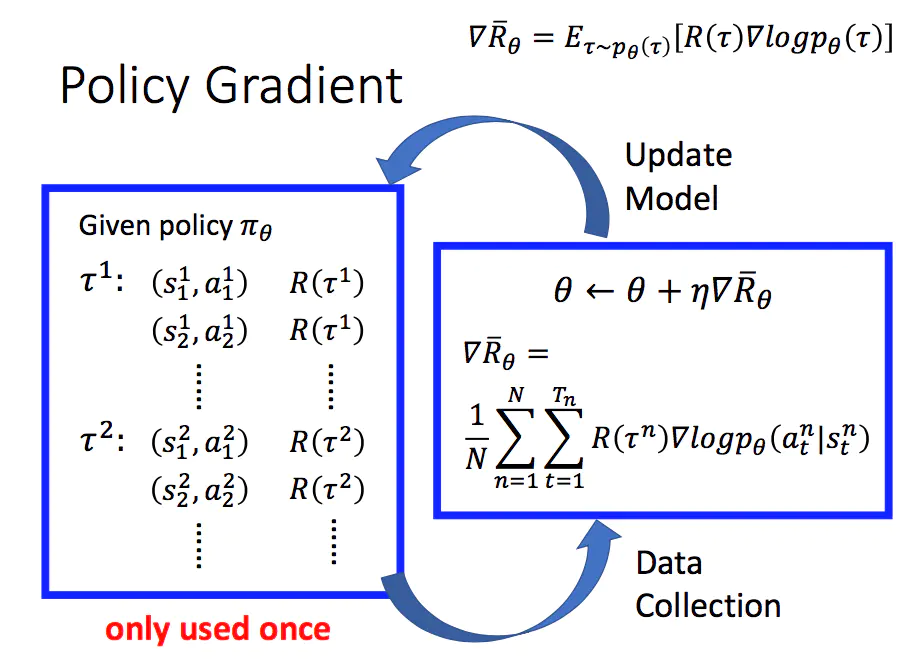
根据按照蒙特卡洛方法近似求期望的原则，可以采样N条轨迹 $\tau$ 并计算每一条轨迹的值，再把每一条轨迹的值加起来除以N取平均，即( $\tau^n$ 上标n代表第n条轨迹，而、则 $a_t^n$ 、 $s_t^n$ 分别代表第n条轨迹里时刻t的动作、状态。

由此可以推导出策略梯度定理

(1)即在采样到的数据里面，采样到在某一个状态 $s_t$ 要执行某一个动作 $a_t$ ， $(s_t, a_t)$ 是在整个轨迹的里面的某一个状态和动作的对。

(2)为了最大化奖励，假设在 $s_t$ 执行 $a_t$ ，最后发现的奖励是正的，就要增加概率。反之，如果在 $s_t$ 执行 $a_t$ 会导致的奖励变成负的，就要减少概率。

(3)用梯度上升来更新参数，原来有一个参数 $\theta$ ，把 $\theta$ 加上梯度 $\nabla\overline{R}_{\theta}$ ，当然要有一个学习率 $\eta$ （类似步长、距离的含义），学习率可用 Adam、RMSProp等方法调整。

2 优势演员-评论家算法

目的：为避免奖励总为正增加基线

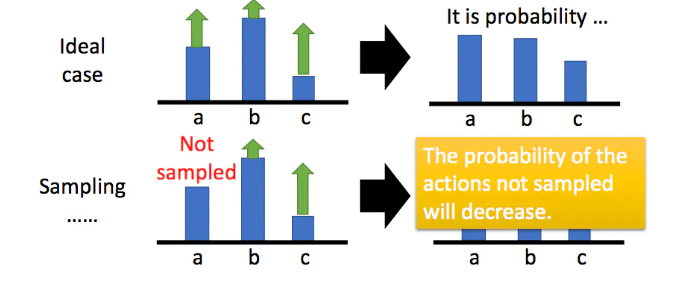
假设某一状态下有三个动作，分别是a,b,c，奖励都是正的。根据公式,我们希望将这三个动作的概率以及对数概率都拉高，但是它们前面的权重不一样，有大有小，所以权重大的，上升的多一点；权重小的，上升的少一些，又因为对数概率是一个概率，三个动作的和要为0，那么在做完归一化后，上升多的才会上升，上升的少的就是下降的。

为了解决奖励总是正的的问题，也为避免方差过大，需要在之前梯度计算的公式基础上加一个基准线b，此b指的baseline。

3. TRPO

信任域策略优化：使用KL散度解决两个分布相差大或步长难以确定的问题。

J_{\mathrm{TRP}0}^{\theta^{\prime}}(\theta)=E_{(s_t,a_t)\sim n_{\theta^{\prime}}}\left[\frac{p_\theta(a_t|s_t)}{p_{\theta^{\prime}}(a_t|s_t)}A^{\theta^{\prime}}(s_t,a_t)\right],\mathrm{KL}\left(\theta,\theta^{\prime}\right)<\delta \tag {3.1}

4. PPO

见PPO详解

参考

[1] John Schulman, Sergey Levine, Pieter Abbeel, Michael Jordan, Philipp Moritz. Trust Region Policy Optimization. In: Proceedings of the 32nd International Conference on Machine Learning (ICML 2015), Lille, France, July 6-11, 2015, ACM, 2015:1889-1897

机器学习之强化学习中的策略学习

# 1 策略梯度算法

# 1.1 算法核心思想

# 1.2 评价标准

# 2 优势演员-评论家算法

# 3. TRPO

# 4. PPO

# 参考