混合专家模型

混合专家模型（Mixture-of-Experts，MoE）为由许多独立网络组成的系统提出了一种新的监督学习过程，每个网络都学习处理完整训练案例集的子集。新过程可以被视为多层监督网络的模块化版本，也可以被视为竞争性学习的关联版本。

1 专家的适应性混合

1991年的论文“Adaptive mixtures of local experts”提出了一种新的监督学习过程，一个系统中包含多个分开的网络，每个网络去处理全部训练样本的一个子集。这种方式可以看做是把多层网络进行了模块化的转换。

假设我们已经知道数据集中存在一些天然的子集（比如来自不同的domain，不同的topic），那么用单个模型去学习，就会受到很多干扰（interference），导致学习很慢、泛化困难。这时，我们可以使用多个模型（即专家expert）去学习，使用一个门网络（Gating Network）来决定每个数据应该被哪个模型去训练，这样就可以减轻不同类型样本之间的干扰。

对于一个样本$c$，第$i$个expert的输出为$o_i^c$，理想的输出是$d^c$，那么损失函数计算如式1.1。

$$E^c={\Vert d^c - \sum\limits_{i}p_i^c o_i^c \Vert}^2 \tag {1.1}$$

其中$p_i^c$是Gating Network分配给每个expert的权重，相当于多个expert齐心协力来得到当前样本$c$的输出。就是让不同的 expert单独计算loss，然后在加权求和得到总体的loss。这样的话，每个专家都有独立判断的能力，而不用依靠其他的expert来一起得到预测结果。如图1.1所示。

图1.1 混合专家模型架构图

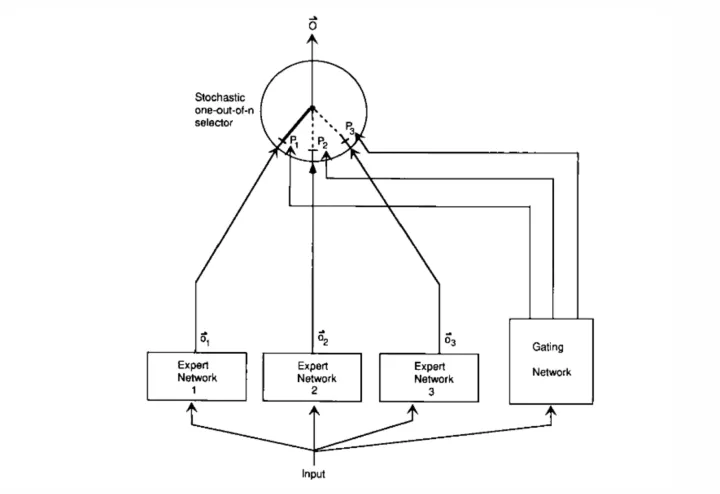
作者在实际做实验的时候，用了一个损失函数的变体，使得效果更好，如式1.2所示。

$$E^c=-log\sum\limits_{i}p_i^ce^{-\frac{1}{2}{\Vert d^c - o_i^c \Vert}^2} \tag {1.2}$$

式1.1的导数，只会跟当前expert有关，但式1.2则还考虑其他experts跟当前sample$c$的匹配程度。

2 稀疏门控混合专家

2017年的论文“Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer”为混合专家模型添加了稀疏门控和token级别的设置，并且应用到RNN中，如图2.1所示。

图1.2 稀疏门控混合专家模型架构图

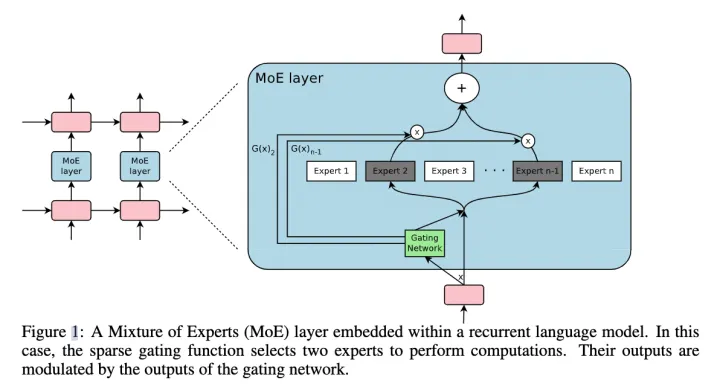
2.1 稀疏门控

设$G(x)$和$E_i(x)$分别是Gating Network和第$i$个expert的输出，那么对于在当前position的输入x，输出就是所有experts的加权和：

$$y = \sum\limits_{i=1}^{n}G(x)_iE_i(x) \tag {2.1}$$

但是这里我们可能有上千个experts，如果每个都算的话，计算量会非常大，所以这里的一个关键就是希望G(x)的输出是稀疏的，只有部分的experts的权重是大于0的，其余等于0的expert直接不参与计算。

首先看传统的Gating Network设计如式2.2所示。

$$G_{\sigma}(x) = Softmax(x \cdot W_g) \tag {2.2}$$

然后，作者加入了 sparsity 和 noise。

$$G(x) = Softmax(KeepTopK(H(x),k)) \tag {2.3}$$

$$H(x)_i = (x \cdot W_g)_i + StandardNormal() \cdot Softplus((x \cdot W_{noise})_i) \tag {2.4}$$

$$KeepTopK(v,k)_i = \left\{ \begin{aligned} &v_i,{v_i\_in\_topK}\\ &-\infty,{otherwise}\\ \end{aligned} \right. \tag {2.5}$$

总而言之，sparsity是通过TopK sampling的方式实现的，对于非TopK的部分，由于值是负无穷，这样在经过softmax之后就会变成0，就相当于关门了。noise项则可以使得不同expert的负载更加均衡。在具体实验中，作者使用的K=2~4.

2.2 token级别

第一篇文章是sample-level的，即不同的样本，使用不同的experts，但是这篇则是token-level的，一个句子中不同的token使用不同的experts。

2.3 专家平衡

作者在实验中发现，不同 experts 在竞争的过程中，会出现“赢者通吃”的现象：前期变现好的 expert 会更容易被 Gating Network 选择，导致最终只有少数的几个 experts 真正起作用。因此作者额外增加了一个 loss，来缓解这种不平衡现象。

$$Importance(X) = \sum\limits_{x \in X}G(x) \tag {2.6}$$

$$L(x) = \lambda \cdot CV(Importance(X))^2 \tag {2.7}$$

其中X代表的是一个batch的样本，把一个batch所有样本的gating weights加起来，然后计算变异系数（coefficient of variation）。总之，这个反映了不同experts之间不平衡的程度。最后这个loss会加到总体loss中，鼓励不同的experts都发挥各自的作用。

3 GShard：Transformer中的MoE

论文“GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding”首次将MoE的思想拓展到Transformer上的工作。具体的做法是，把Transformer的encoder和decoder中，每隔一个（every other）的FFN层，替换成position-wise的 MoE层，使用的都是Top-2 Gating Network。

图3.1 Transformer中的混合专家模型

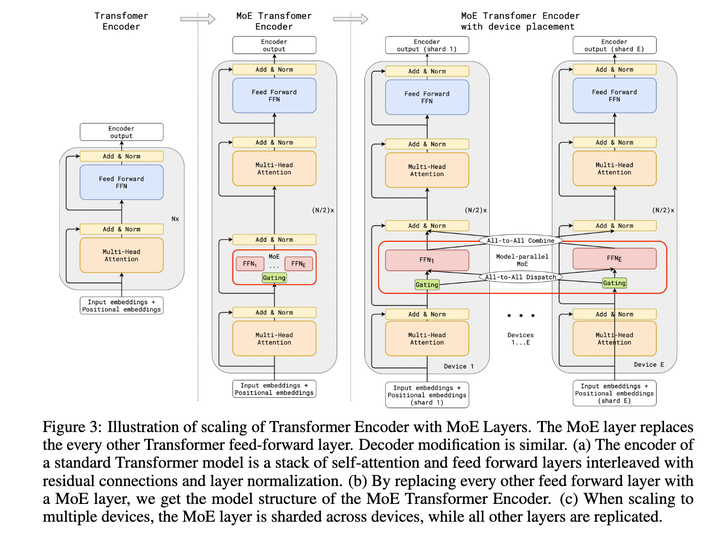
文中还提到了很多其他设计：

（1）Expert capacity balancing：强制每个expert处理的tokens数量在一定范围内。

（2）Local group dispatching：通过把一个batch内所有的tokens分组，来实现并行化计算。

（3）Auxiliary loss：也是为了缓解“赢者通吃”问题。

（4）Random routing：在Top-2 gating的设计下，两个expert如何更高效地进行routing。